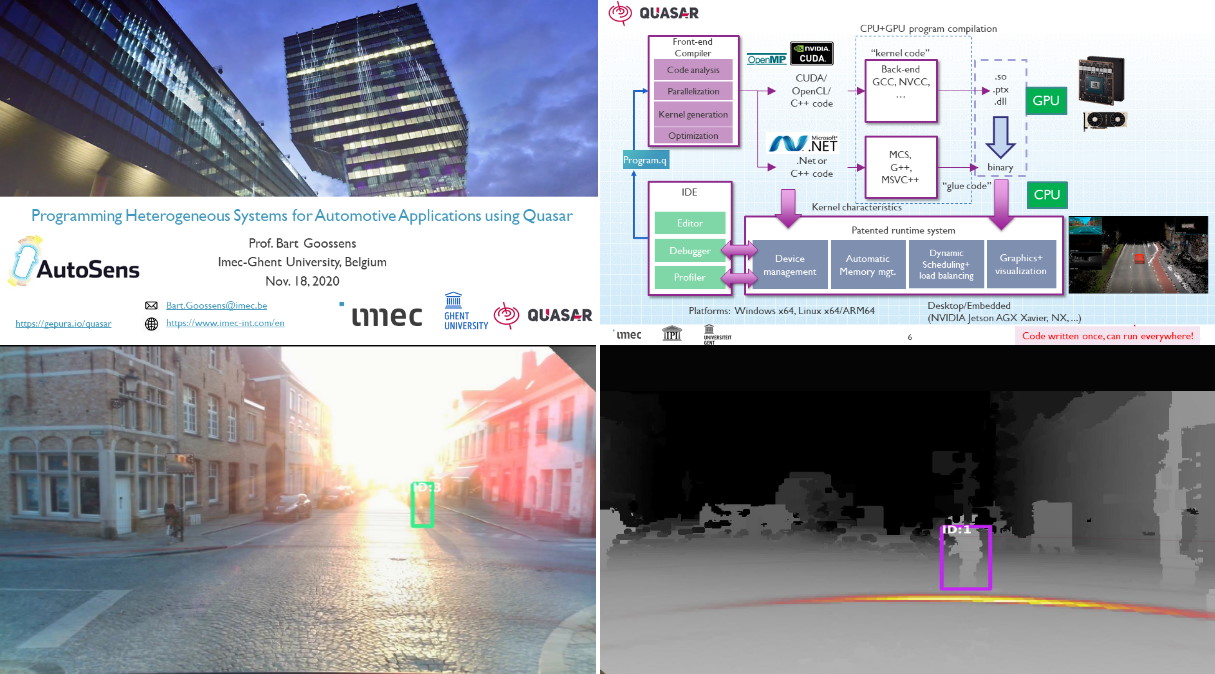
Real-time Waste Classification using Quasar
In a collaboration with VITO, Suez and Umicore and with support of EIT Raw Materials, we designed a waste classification algorithm which was fully implemented in Quasar. High-speed and real-time processing were part of the requirement, the conveyor belt rolls at a fast, industrial speed. Therefore, the sensors must be able to analyze the waste streams quickly enough, just like the software and algorithms have to process all measurements within a few seconds. The faster you can process data, the more waste you can characterize in a short time. Working faster also means quicker calculations, so we had to optimize the processing speed of the algorithms.
By using Quasar technology, the critical part of the processing chain could be off-loaded to the GPU, and a processing speed was obtained that is 133 times faster than a CPU-only implementation.
Read the full article here.
AutoSens 2020
We will be at AutoSens 2020 on Wed Nov 18, 4:55 PM – 5:20 PM GMT +0 / 5:55 PM – 6:20 PM CEST !

We will discuss some key programming principles for heterogeneous systems, in particular how to optimize across components (on the low-level image processing level and on the system level) to answer questions such as above. We present our own Quasar compiler and programming framework for this purpose. We will demonstrate our latest Radar-RGB sensor fusion results.
For more information: click here. See you there!
Quasar Technology Powers Nedinsco’s Depth View Pro Vision System
A result of our successful collaboration with the companies Invenira and Nedinsco: the Depth View Pro camera offers an extended depth-of-field to capture 3D objects. The processing speed of 25 fps for 5 MP images is made possible thanks to Quasar acceleration!
A small demonstration of the image quality is given below:
More information on this product can be found on the Depth View Pro product page.
Quasar showcase: Interactive ImageJ plugin for Restoration of 3D Electron Microscopy
The Flemish Institute for Biotechnology (VIB) has just released an interactive ImageJ plugin for restoration of 3D electron microscopy. The plugin was realized entirely using the Gepura/Quasar software! In fact, the Quasar runtime takes care of the GPU acceleration, giving tremendous speedups compared to multi-core CPU code! A scientific paper discussing the results of this research also appeared in Nature last Friday (Feb. 7, 2020):
Strategic collaboration between imec/Ghent University and Invenira
Realtime lens distortion corrections on UltraHD 4k video streams using Quasar

Quasar was used at imec Ghent to perform realtime lens distortion corrections on UltraHD 4k video streams.
Because the quality of digital image sensors often outperforms the quality of optical lens systems, the sensors capture various distortions (such as chromatic aberration, noise, blur and various other unwanted effects). Now, software comes in for an effective quality compensation at affordable cost. Before, lens correction algorithms were only available for offline processing (e.g., in software like Photoshop), but now, with use of GPUs and the Quasar software, the algorithms could easily be developed and tested in real-time. On a PC platform with GPU, UltraHD 4k video could be processed at 30 fps.
Read more in the imec Magazine article from April 2019.
Real-time SDR to HDR video conversion using Quasar
The conversion from low-dynamic range video to high dynamic range content that can be displayed on, e.g., high dynamic range TVs, faces several obstacles: dealing with artifacts such as ‘ghost’ and ‘halo’ images, recognizing bright objects in dark environments, converting light and dark settings in a visually distinct way and carrying out all of these calculations in real-time on a GPU. Existing software solutions struggle with these problems and are unable to achieve the required quality in the end result.
By automatically handling the mapping from algorithm to GPU, Quasar allows application specialists to focus on the application at hand, focusing on the quality of the algorithms rather than hardware specific details. At the same time the algorithm can be tested on high resolution datasets and in realtime. This led to the development of a SDR->HDR conversion algorithm, from which the result can be inspected below.

Left – visual artifacts occurring during traditional conversion to HDR. Right – processing result of software developed using Quasar
Read more in the imec magazine.
See also our previous blog post from February, with a video example.
New Feature in Quasar: Cooperative Thread Groups
The latest release of Quasar now offers support for CUDA 9 cooperative groups. Below, we describe how cooperative groups can be used from Quasar. Overall, cooperative threading brings some interesting optimization possibilities for Quasar kernel functions.
1 Synchronization granularity
The keyword syncthreads now accepts a parameter that indicates which threads are being synchronized. This allows more fine grain control on the synchronization.
| Keyword | Description |
|---|---|
syncthreads(warp) |
performs synchronization across the current (possibly diverged) warp (32 threads) |
syncthreads(block) |
performs synchronization across the current block |
syncthreads(grid) |
performs synchronization across the entire grid |
syncthreads(multi_grid) |
performs synchronization across the entire multi-grid (multi-GPU) |
syncthreads(host) |
synchronizes all host (CPU and GPU threads) |
The first statement syncthreads(warp) allows divergent threads to synchronize at any time (it is also useful in the context of Volta’s independent scheduling). syncthreads(block) is equivalent to syncthreads in previous versions of Quasar. The grid synchronization primitive syncthreads(grid) is particularly interesting, it is a feature of CUDA 9 that was not available before. It allows to place barriers inside kernel function that synchronize all blocks. The following function:
function y = gaussian_filter_separable(x, fc, n)
function [] = __kernel__ gaussian_filter_hor(x : cube, y : cube, fc : vec, n : int, pos : vec3)
sum = 0.
for i=0..numel(fc)-1
sum = sum + x[pos + [0,i-n,0]] * fc[i]
endfor
y[pos] = sum
endfunction
function [] = __kernel__ gaussian_filter_ver(x : cube, y : cube, fc : vec, n : int, pos : vec3)
sum = 0.
for i=0..numel(fc)-1
sum = sum + x[pos + [i-n,0,0]] * fc[i]
end
y[pos] = sum
end
z = uninit(size(x))
y = uninit(size(x))
parallel_do (size(y), x, z, fc, n, gaussian_filter_hor)
parallel_do (size(y), z, y, fc, n, gaussian_filter_ver)
endfunctionCan now be simplified to:
function y = gaussian_filter_separable(x, fc, n)
function [] = __kernel__ gaussian_filter_separable(x : cube, y : cube, z : cube, fc : vec, n : int, pos : vec3)
sum = 0.
for i=0..numel(fc)-1
sum = sum + x[pos + [0,i-n,0]] * fc[i]
endfor
z[pos] = sum
syncthreads(grid)
sum = 0.
for i=0..numel(fc)-1
sum = sum + z[pos + [i-n,0,0]] * fc[i]
end
y[pos] = sum
endfunction
z = uninit(size(x))
y = uninit(size(x))
parallel_do (size(y), x, y, z, fc, n, gaussian_filter_separable)
endfunctionThe advantage is not only in the improved readability of the code, but the number of kernel function calls can be reduced which further increases the performance. Note: this feature requires at least a Pascal GPU.
2 Interwarp communication
New special kernel function parameters (similar to blkpos, pos etc.) will be added to control the GPU threads.
| Parameter | Type | Description |
|---|---|---|
coalesced_threads |
thread_block |
a thread block of coalesced threads |
this_thread_block |
thread_block |
describes the current thread block |
this_grid |
thread_block |
describes the current grid |
this_multi_grid |
thread_block |
describes the current multi-GPU grid |
The new thread_block class will have the following methods.
| Method | Description |
|---|---|
sync() |
Synchronizes all threads within the thread block |
partition(size : int) |
Allows partitioning a thread block into smaller blocks |
shfl(var, src_thread_idx : int) |
Direct copy from another thread |
shfl_up(var, delta : int) |
Direct copy from another thread, with index specified relatively |
shfl_down(var, delta : int) |
Direct copy from another thread, with index specified relatively |
shfl_xor(var, mask : int) |
Direct copy from another thread, with index specified by a XOR relative to the current thread index |
all(predicate) |
Returns true if the predicate for all threads within the thread block evaluates to non-zero |
any(predicate) |
Returns true if the predicate for any thread within the thread block evaluates to non-zero |
ballot(predicate) |
Evaluates the predicate for all threads within the thread block and returns a mask where every bit corresponds to one predicate from one thread |
match_any(value) |
Returns a mask of all threads that have the same value |
match_all(value) |
Returns a mask only if all threads that share the same value, otherwise returns 0. |
In principle, the above functions allow threads to communicate with each other. The shuffle operations allow taking values from other active threads (active means not disabled due to thread divergence). all, any, ballot, match_any and match_all allow to determine whether the threads have reached a given state.
The warp shuffle operations require a Kepler GPU and allow the use of shared memory to be avoided (register access is faster than shared memory). This may bring again performance benefits for computationally intensive kernels such as convolutions and parallel reductions (sum, min, max, prod etc.).
Using this functionality will require the CUDA target to be specified explicitly (i.e., the functionality cannot be easily simulated by the CPU). This may be obtained by placing the following code attribute inside the kernel: {!kernel target="nvidia_cuda"}. For CPU execution a separate kernel needs to be written. Luckily, several of the warp shuffling optimizations can be integrated in the compiler optimization stages, so that only one single kernel needs to be written.
Quasar at the Design, Automation and Test in Europe (DATE’18) conference in Dresden
The Three Function Types of Quasar from a Technical Perspective
To give programmers ultimate control on the acceleration of functions on compute devices (GPU, multi-core CPU), Quasar has three distinct function types:
- Host Functions: host functions are the default functions in Quasar. Depending on the compilation target, they are either interpreted or compiled to binary CPU code. Host functions run on the CPU and form a glue for the code that runs on other devices. When host functions contain for-loops, these loops are (when possible) automatically parallelized by the Quasar compiler. The parallelized version then runs on multi-core CPU or GPU; what happens in the background is that a kernel function is generated. Within the Quasar Redshift IDE, host functions are interpreted, which also allows stepping through the code and putting breakpoints.
- Kernel Functions: given certain data dimensions, kernel functions specify what needs to be done to each element of the data. The task can be either a parallel task or a serial task. Correspondingly, kernel functions are launched either using the
parallel_dofunction or using theserial_dofunction:function [] = __kernel__ filter(image, pos) ... endfunction parallel_do(size(image),image,filter)In the above example, the kernel function
filteris applied in parallel to each pixel component of the imageimage. The first parameter ofparallel_do/serial_dois always the data dimension (i.e., the size of the data). The last parameter is the kernel function to be called, and in the middle are the parameters to be passed to the kernel function.posis a special kernel function parameter that indicates the position within the data (several other parameters exist, such asblkpos,blkdimetc., see the documentation for a detailed list).Kernel functions can call other kernel functions, but only through
serial_doand/orparallel_do. The regular function calling syntax (direct call, i.e, withoutserial_do/parallel_do) on kernel functions is not permitted. This is because kernel functions have other infrastructure (e.g., shared memory, device-specific parameters) which would cause conflicts when kernel functions would call each other. - Device functions: in contrast to host functions, device functions (indicated with
__device__) are intended to be natively compiled using the back-end compiler. They can be seen as auxiliary functions that can be called from either kernel functions, device functions or even host functions (note that a kernel function cannot call a host function). The compiler back-end may generate C++, CUDA or OpenCL code that is then further compiled to binary code to be executed on CPU and/or GPU. Currently, apart from the CPU there are no accelerators that can run a device function directly when called from a host function. This means, for a GPU, the only way to call a device function is through a kernel function.function y = __device__ norm(vector : vec) y = sqrt(sum(vector.^2)) endfunction
Functions in Quasar are first-class variables. Correspondingly, they have a data type. Below are some example variable declarations:
host : [(cube, cube) -> scalar]
filter : [__kernel__ (cube) -> ()]
norm : [__device__ (vec) -> scalar]This allows passing functions to other functions, where the compiler can statically check the types. Additionally, to prevent functions from being accessed unintendedly, functions can be nested. For example, a gamma correction operation can be implemented using a host function containing a kernel function.
function y : mat = gamma_correction(x : mat, gamma_fn : [__device__ scalar->scalar])
function [] = __kernel__ my_kernel(gamma_fn : [__device__ scalar->scalar], x : cube, y : cube, pos : ivec2)
y[pos] = gamma_fn(x[pos])
endfunction
y = uninit(size(x)) % Allocation of uninitialized memory
parallel_do(size(x), gamma_fn, x, y, my_kernel)
endfunctionBecause functions support closures (i.e., they capture the variable values of the surround contexts at the moment the function is defined), the above code can be simplified to:
function y : mat = gamma_correction(x : mat, gamma_fn : [__device__ scalar->scalar])
function [] = __kernel__ my_kernel(pos : ivec2)
y[pos] = gamma_fn(x[pos])
endfunction
y = uninit(size(x))
parallel_do(size(x), my_kernel)
endfunctionOr even in shorter form, using lambda expression syntax:
function y : mat = gamma_correction(x : mat, gamma_fn : [__device__ scalar->scalar])
y = uninit(size(x))
parallel_do(size(x), __kernel__ (pos) -> y[pos] = gamma(x[pos]))
endIn many cases, the type of the variables can safely be omitted (e.g., pos in the above example) because the compiler can deduce it from the context.
Now, experienced GPU programmers may wonder about the performance cost of a function pointer call from a kernel function. The good news is that the function pointer call is avoided, by automatic function specialization (a bit similar to template instantiation in C++). With this mechanism, device functions passed via the function parameters or closure can automatically be inlined in a kernel function.
function y = gamma_correction(x, gamma_fn)
y = uninit(size(x))
parallel_do(size(x), __kernel__ (pos) -> y[pos] = gamma(x[pos]))
end
gamma = __device__ (x) -> 255*(x/255)^2.4
im_out = gamma_correction(im_in, gamma)This will cause the following kernel function to be generated, behind the hood:
function [] = __kernel__ opt__gamma_correction(pos:int,y:vec,x:vec)
% Inlining of function 'gamma' with parameters 'x'=x[pos]
y[pos]=(255*((x[pos]/255)^2.4))
endfunctionAnother optimization was performed in the background: kernel flattening. Because each element of the data is accessed separately, the data is processed as a vector (using raster scanning) rather than as a matrix (or cube) representation. This entirely eliminates costly index calculations.
Summarizing, three function types offer the flexibility of controlling on which target devices (CPU or GPU) certain code fragments might run, while offering a unified programming interface: the code written for GPU can be executed on CPU as well, thereby triggering other target-specific optimizations.